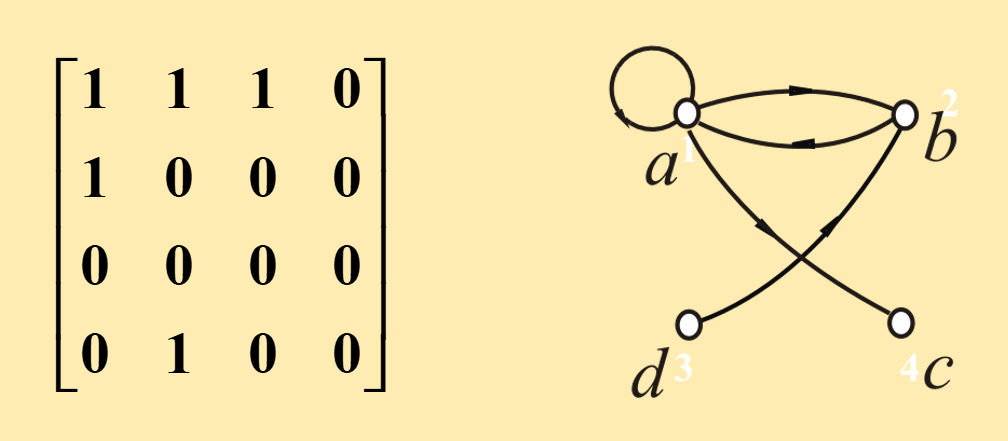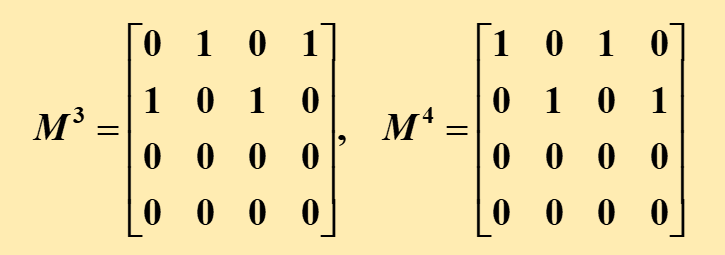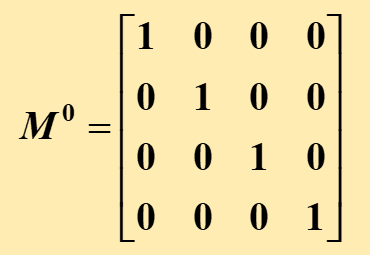离散数学-Week5

证明方法

命题的提出过程

观察与猜想

通过观察具体实例提出一般性命题：

观察实例：

• 1 = 1²
• 1 + 3 = 2²
• 1 + 3 + 5 = 3²
• 1 + 3 + 5 + 7 = 4²
• … …

猜想： 前n个奇数之和等于n²，即：

\[1+3+5+⋯+(2n−1) = n²\]

数学归纳法

命题形式

\[∀x(x∈N∧x≥n0​),P(x)\]

数学归纳法的步骤

1. 归纳基础：证明P(n₀)为真
2. 归纳步骤：$\forall x(x \geq n_0)$，假设P(x)为真，证明P(x+1)为真

说明： “P(x)为真”称为归纳假设

例9：奇数和的证明

命题： 对所有n ≥ 1，$1 + 3 + 5 + \cdots + (2n - 1) = n²$
证明：

• 归纳基础：当n = 1时，1 = 1²，结论成立

• 归纳步骤：假设对n ≥ 1结论成立，则有：

  \[1+3+5+⋯+(2n−1)+(2n+1) = n²+(2n+1) = (n+1)²\]

  得证当n + 1时结论也成立

重要注意： 归纳基础与归纳步骤两者缺一不可

归纳法的误用与反例

反例1：错误的归纳证明

命题： $\forall n \geq 1, 2^1 + 2^2 + \cdots + 2^n = 2^{n+1}$
错误证明：
假设$\forall n \geq 1$结论成立，则：

\[2^1 + 2^2 + ⋯ + 2^n + 2^{n+1} = 2^{n+1} + 2^{n+1} = 2^{n+2}\]

对n + 1结论成立

问题： 缺少归纳基础验证，实际上该命题不成立

反例2：错误的素数判定猜想

观察： $2^{n-1} - 1$是否被n整除
错误猜想： 设n ≥ 3，n是素数的充分必要条件是$2^{n-1} - 1$被n整除
反例： 561 = 3 × 11 × 17是合数，但$2^{560} - 1$能被561整除

第一数学归纳法 vs 第二数学归纳法

第二数学归纳法（强归纳法）

1. 归纳基础：证明P(n₀)为真
2. 归纳步骤：$\forall x(x \geq n_0)$，假设P(n₀), P(n₀+1), …, P(x)为真，证明P(x+1)为真

归纳假设： $\forall y(n_0 \leq y \leq x), P(y)$为真

多米诺骨牌比喻

• 第一归纳法：第一个牌会倒，且前一张牌倒则后一张牌必定会倒
• 第二归纳法：前一批牌会倒，且前一批牌倒则紧接着的下一张牌必定会倒
  第二归纳法把一批牌看作一张牌，初始条件由一张牌变成了一批牌

第二数学归纳法应用实例

例10：整数的素数分解

命题： 任何大于等于2的整数均可表成素数的乘积
证明：

• 归纳基础：对于2，结论显然成立
• 归纳步骤：假设对所有的k(2 ≤ k ≤ n)结论成立，要证结论对n + 1也成立
  • 若n + 1是素数，则结论成立
  • 否则n + 1 = ab，其中2 ≤ a, b < n
  • 由归纳假设，a, b均可表成素数的乘积
  • 从而n + 1也可表成素数的乘积
  • 得证结论对n + 1成立

例11：邮票组合问题

命题： 可用4分和5分邮票组成n分邮资，n ≥ 12
证明：

• 归纳基础：
  • 12 = 3 × 4
  • 13 = 2 × 4 + 5
  • 14 = 2 × 5 + 4
  • 15 = 3 × 5
    得证对n = 12, 13, 14, 15时结论成立
• 归纳步骤：设n ≥ 15，假设对12, 13, …, n结论成立
  • 由12 ≤ n - 3 < n和归纳假设，n - 3分邮资可用4分和5分邮票组成
  • 再加一张4分邮票即可得到n + 1分邮资
  • 得证结论对n + 1也成立

特殊证明方法

空证明法（前件假证明法）

做法： 证明A恒为假
例： 设n ∈ N，记P(n): 若n > 1，则n² > 1。证明P(0)为真

• P(0): 若0 > 1，则0² > 1
• 由于0 > 1恒假，因此蕴含式恒真

平凡证明法（后件真证明法）

做法： 证明B恒为真，而不需要假设A为真 例： 若a ≤ b，则a⁰ ≤ b⁰

• 由于a⁰ = b⁰ = 1，结论恒真

应用： 常在归纳证明的归纳基础中出现

递归定义

递归定义的基本概念

递归定义是数理逻辑和计算机科学中常用的一种定义方式，使用被定义对象的自身来为其下定义（简单说就是自我复制的定义）。

递归定义（recursive definition）亦称归纳定义，是一种实质定义，指用递归的方法给一个概念下的定义。

递归定义示例

幂运算的递归定义

例如，$a^n$ 可以递归定义如下：

• $a^0 = 1$
• $a^n = a^{n-1} \cdot a$，$n = 1, 2, \ldots$

例1.12：斐波那契数列

斐波那契数列 ${f_n}$ 递归定义如下：

• $f_0 = 1$, $f_1 = 1$
• $f_n = f_{n-1} + f_{n-2}$，$n = 2, 3, \ldots$

计算得：
$f_0 = 1$, $f_1 = 1$, $f_2 = 2$, $f_3 = 3$, $f_4 = 5$, $f_5 = 8$, $f_6 = 13$, $\ldots$

例1.13：集合的递归定义

集合 $A$ 的递归定义如下：

1. $3 \in A$
2. 若 $x, y \in A$，则 $x + y \in A$
3. 只有有限次使用 (1) 和 (2) 得到的数属于 $A$

结果：$A = {3n \mid n \in \mathbb{Z}^+}$

例1.14：算术表达式的归纳定义

算术表达式的归纳定义如下：

1. 任何实数和变量都是算术表达式
2. 如果 $f, g$ 是算术表达式，则 $(f+g)$, $(f-g)$, $(f \cdot g)$ 是算术表达式
3. 如果 $f, g$ 是算术表达式且 $g \neq 0$，则 $(f/g)$ 是算术表达式
4. 如果 $f$ 是算术表达式，则 $\forall n \in \mathbb{Z}^+$, $(f↑n)$ 是算术表达式
5. 只有有限次使用 (1)~(4) 得到的式子是算术表达式

算术表达式示例

根据上述定义，以下都是合法的算术表达式：

• $((3 \cdot x) - 1)$
• $(((2 \cdot (x^2)) + (5 \cdot x)) - 4)$
• $(((x + y) - z) / (5 + x))$

递归定义的特点

1. 基础情况：明确定义最简单的情况
2. 递归规则：用较简单的情况定义较复杂的情况
3. 封闭性：只有通过有限次应用前两条规则得到的对象才属于被定义的集合

函数、关系与集合

基本概念

集合

• 定义：具有某种特定性质的对象的总体
• 特点：可以是有限的，也可以是无限的
• 元素：集合中的每个对象称为元素

函数

• 定义：描述了两个集合之间的对应关系
• 本质：一种输入和输出之间的关系
• 定义域：自变量的集合
• 值域：因变量的集合

关系

• 定义：集合之间的联系，描述元素之间的某种属性或特征
• 特点：
  • 可以是函数，也可以是非函数
  • 如果一个关系中的每个输入值都对应唯一的输出值，则该关系是一个函数
  • 关系可以是一对一、一对多或多对多

三者之间的联系

函数、关系、集合是数学中的基本概念，它们之间有着密切的联系：

1. 集合是基础：集合是函数和关系的基础，是数学中研究对象的基本单位
2. 函数是特殊关系：函数是一种特殊的关系，描述输入和输出之间的对应关系
3. 相互依存：函数、关系、集合相互依存、相互支撑，共同构成了数学的丰富内涵

通过对函数、关系、集合的研究，能够更好地理解数学中的各种概念和定理，进而应用到实际问题中。

关系

关系的定义及其表示

有序对与笛卡尔积

有序对

定义4.1：由两个元素，如x和y，按照一定的顺序组成的二元组称为有序对，记作 <x,y>，其中x是第一元素，y是第二元素。

实例：点的直角坐标 (3,-4)

有序对的性质：

• 有序性：<x,y> ≠ <y,x>（当x ≠ y时）
• 相等条件：<x,y> = <u,v> ⇔ x = u ∧ y = v

例1：<2,x+5> = <3y-4,y>，求x, y
解：3y-4=2, x+5=y ⇒ y=2, x=-3

笛卡尔积

定义4.2：设A, B为集合，A与B的笛卡尔积记作A×B，

\[A×B = \{<x,y>∣x∈A∧y∈B\}\]

例2：
A={0, 1}, B={a, b, c}

• A×B={<0,a>,<0,b>,<0,c>,<1,a>,<1,b>,<1,c>}
• B×A={<a,0>,<b,0>,<c,0>,<a,1>,<b,1>,<c,1>}
• A={∅}, B=∅
• P(A)×A={<∅,∅>, <{∅},∅>}
• P(A)×B=∅

笛卡尔积的性质：

1. 若A或B中有一个为空集，则A×B就是空集 A×∅=∅×B=∅A×∅ = ∅×B = ∅A×∅=∅×B=∅
2. 不适合交换律：A×B ≠ B×A（当A≠B, A≠∅, B≠∅）
3. 不适合结合律：(A×B)×C ≠ A×(B×C)（当A≠∅, B≠∅, C≠∅）
4. 对于并或交运算满足分配律：
   • A×(B∪C) = (A×B)∪(A×C)
   • (B∪C)×A = (B×A)∪(C×A)
   • A×(B∩C) = (A×B)∩(A×C)
   • (B∩C)×A = (B×A)∩(C×A)
5. 若|A|=m, |B|=n, 则|A×B|=mn

有序n元组和n阶笛卡尔积

定义4.3：

1. 由n个元素x₁, x₂, …, xₙ按照一定的顺序排列构成有序n元组，记作<x₁, x₂, …, xₙ>
2. 设A₁, A₂, …, Aₙ为集合，称

\[A₁​×A₂​×…×Aₙ​=\{<x₁​,x₂​,…,xₙ​>∣xᵢ​∈Aᵢ​,i=1,2,…,n\}\]

为n阶笛卡尔积

实例：(1,1,0)为空间直角坐标，(1,1,0)∈R×R×R

二元关系的定义

定义4.4：如果一个集合满足以下条件之一：

1. 集合非空，且它的元素都是有序对
2. 集合是空集
   则称该集合为一个二元关系，简称为关系，记作R。

如<x,y>∈R，可记作xRy；如果<x,y>∉R，则记作x̸Ry

实例：

• R={<1,2>,<a,b>}是二元关系
• S={<1,2>,a,b}不是二元关系（当a,b不是有序对时）

例3：

1. R={<x,y> | x,y∈N, x+y<3}
   = {<0,0>,<0,1>,<0,2>,<1,0>,<1,1>,<2,0>}
2. C={<x,y> | x,y∈R, x²+y²=1}，C是直角坐标平面上点的横、纵坐标之间的关系，构成单位圆
3. R={<x,y,z> | x,y,z∈R, x+2y+z=3}，代表空间直角坐标系中的一个平面

从A到B的关系与A上的关系

定义4.5：

• 设A,B为集合，A×B的任何子集所定义的二元关系叫做从A到B的二元关系
• 当A=B时则叫做A上的二元关系

例4：
A={0,1}, B={1,2,3}

• R₁={<0,2>}, R₂=A×B, R₃=∅, R₄={<0,1>}
• 从A到B的关系：R₁, R₂, R₃, R₄
• A上的关系：R₃和R₄

计数：

• |A|=n, |B|=m, |A×B|=nm
• A×B的子集有2ⁿᵐ个
• 从A到B有2ⁿᵐ个不同的二元关系
• |A|=n, A上有2ⁿ^²个不同的二元关系
• 例如|A|=3, 则A上有512个不同的二元关系

A上重要关系的实例

设A为任意集合：

定义4.6：

• 空关系：∅是A上的关系
• 全域关系：E_A = {<x,y> | x∈A ∧ y∈A} = A×A
• 恒等关系：I_A = {<x,x> | x∈A}

例：A={1,2}

• E_A={<1,1>,<1,2>,<2,1>,<2,2>}
• I_A={<1,1>,<2,2>}

定义4.7：

• 小于等于关系：L_A = {<x,y> | x,y∈A ∧ x≤y}，A⊆R
• 整除关系：D_A = {<x,y> | x,y∈A ∧ x整除y}，A⊆Z*
• 包含关系：R⊆ = {<x,y> | x,y∈A ∧ x⊆y}，A是集合族

例：
A={1,2,3}

• Lₐ={<1,1>,<1,2>,<1,3>,<2,2>,<2,3>,<3,3>}
• Dₐ={<1,1>,<1,2>,<1,3>,<2,2>,<3,3>}
• A=P(B)={∅,{a},{b},{a,b}}，则A上的包含关系：
  R⊆={<∅,∅>,<∅,{a}>,<∅,{b}>,<∅,{a,b}>,<{a},{a}>
  ,<{a},{a,b}>,<{b},{b}>,<{b},{a,b}>,<{a,b},{a,b}>}

类似的还可以定义大于等于关系、小于关系、大于关系、真包含关系等。

二元关系的表示

表示方式：关系的集合表达式、关系矩阵、关系图

定义4.8 关系矩阵：
若A={x₁, x₂, …, xₘ}，B={y₁, y₂, …, yₙ}，R是从A到B的关系，R的关系矩阵是布尔矩阵Mᵣ = [rᵢⱼ]ₘ×ₙ，其中

\[rᵢⱼ=1⟺<xᵢ​,yⱼ​\>∈R\]

定义4.9 关系图：
若A={x₁, x₂, …, xₘ}，R是A上的关系，R的关系图是Gᵣ=<A, R>，其中A为结点集，R为边集。如果<xᵢ,xⱼ>∈R，在图中就有一条从xᵢ到xⱼ的有向边。 注意：

• 关系矩阵适合于表示从A到B的关系或者A上的关系
• 关系图适合于表示A上的关系

例5：
A={a, b, c, d}, R={<a,a>,<a,b>,<a,c>,<b,a>,<d,b>}

R的关系矩阵Mᵣ和关系图Gᵣ如下：

关系的基本运算

定义域、值域和域

定义4.10：设R是二元关系

1. 定义域：R中所有有序对的第一元素构成的集合，记作domR

\[domR=\{x∣∃y(<x,y\>∈R)\}\]

1. 值域：R中所有有序对的第二元素构成的集合，记作ranR

\[ranR=\{y∣∃x(<x,y>∈R)\}\]

1. 域：R的定义域和值域的并集，记作fldR

\[fldR=domR∪ranR\]

例1：
设 $R = { <a,{b}>, <c,d>, <{a},{d}>, <d,{d}> }$，则：

• $\text{dom}R = { a, c, {a}, d }$
• $\text{ran}R = { {b}, d, {d} }$
• $\text{fld}R = { a, c, {a}, d, {b}, {d} }$

逆关系

定义4.11：R的逆关系，简称R的逆

\[R^{-1}={<y,x\>∣<x,y\>∈R}\]

关系合成

定义4.12：R与S的合成

\[R∘S={<x,z>∣∃y(<x,y>∈R∧<y,z>∈S)}\]

例2：
设：

• $R = { <1,2>, <2,3>, <1,4>, <2,2> }$
• $S = { <1,1>, <1,3>, <2,3>, <3,2>, <3,3> }$

则：

• $R^{-1} = { <2,1>, <3,2>, <4,1>, <2,2> }$
• $R \circ S = { <1,3>, <2,2>, <2,3> }$
• $S \circ R = { <1,2>, <1,4>, <3,2>, <3,3> }$

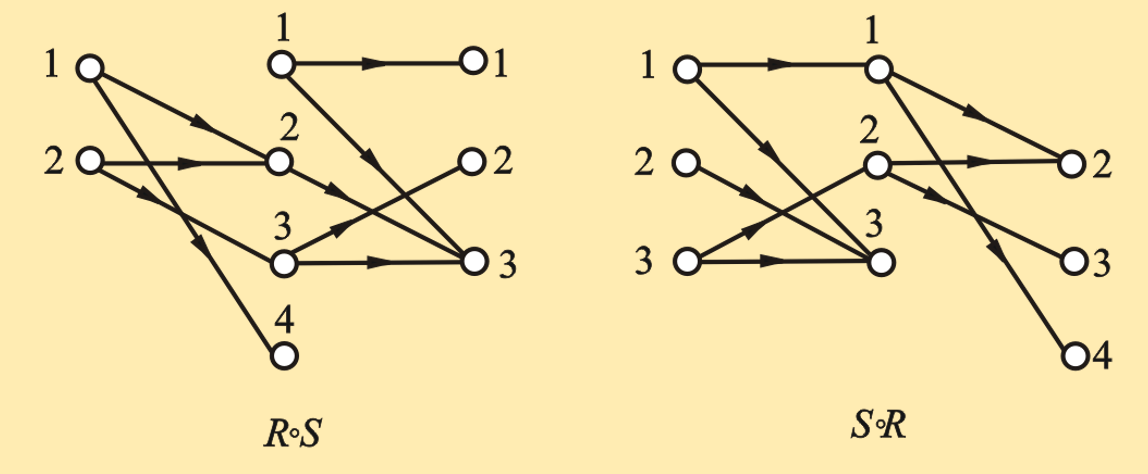
合成运算的图示方法

利用图示（不是关系图）方法求合成： 对于：

• $R = { <1,2>, <2,3>, <1,4>, <2,2> }$
• $S = { <1,1>, <1,3>, <2,3>, <3,2>, <3,3> }$

R∘S的计算过程：

• <1,2>∈R 且 <2,3>∈S ⇒ <1,3>∈R∘S
• <2,3>∈R 且 <3,2>∈S ⇒ <2,2>∈R∘S
• <2,3>∈R 且 <3,3>∈S ⇒ <2,3>∈R∘S
• <2,2>∈R 且 <2,3>∈S ⇒ <2,3>∈R∘S

∴ $R \circ S = { <1,3>, <2,2>, <2,3> }$

S∘R的计算过程：

• <1,1>∈S 且 <1,2>∈R ⇒ <1,2>∈S∘R
• <1,1>∈S 且 <1,4>∈R ⇒ <1,4>∈S∘R
• <3,2>∈S 且 <2,2>∈R ⇒ <3,2>∈S∘R
• <3,2>∈S 且 <2,3>∈R ⇒ <3,3>∈S∘R

∴ $S \circ R = { <1,2>, <1,4>, <3,2>, <3,3> }$

基本运算的性质

定理4.1 设F是任意的关系：

1. $(F⁻¹)⁻¹ = F$
2. $domF⁻¹ = ranF, ranF⁻¹ = domF$

证明：
(1) 任取<x,y>：

\[<x,y>∈(F−1)−1⇔<y,x>∈F−1⇔<x,y>∈F\]

∴ $(F⁻¹)⁻¹ = F$

(2) 任取x：

\[x∈domF−1⇔∃y(<x,y>∈F−1)⇔∃y(<y,x>∈F)⇔x∈ranF\]

∴ $domF⁻¹ = ranF$，同理$ranF⁻¹ = domF$

定理4.2 设F, G, H是任意的关系：

1. (F∘G)∘H = F∘(G∘H)
2. (F∘G)⁻¹ = G⁻¹∘F⁻¹

证明：
(1) 任取<x,y>：

<x,y>∈(F∘G)∘H
​⇔∃t(<x,t>∈F∘G∧<t,y>∈H)
⇔∃t(∃s(<x,s>∈F∧<s,t>∈G)∧<t,y>∈H)
⇔∃t∃s(<x,s>∈F∧<s,t>∈G∧<t,y>∈H)
⇔∃s(<x,s>∈F∧∃t(<s,t>∈G∧<t,y>∈H))
⇔∃s(<x,s>∈F∧<s,y>∈G∘H)⇔<x,y>∈F∘(G∘H)​

∴ (F∘G)∘H = F∘(G∘H)

(2) 任取<x,y>：

<x,y>∈(F∘G)−1
​⇔<y,x>∈F∘G
⇔∃t(<y,t>∈F∧<t,x>∈G)
⇔∃t(<x,t>∈G−1∧<t,y>∈F−1)
⇔<x,y>∈G−1∘F−1​

∴ (F∘G)⁻¹ = G⁻¹∘F⁻¹

定理4.3 设R为A上的关系：

\[R∘I_A​=I_A​∘R=R\]

证明：
任取<x,y>：

<x,y>∈R∘IA
​⇔∃t(<x,t>∈R∧<t,y>∈IA​)
⇔∃t(<x,t>∈R∧t=y∧y∈A)
⇔<x,y>∈R

∴ R∘I_A = R，同理I_A∘R = R

关系的幂运算

幂运算的定义

定义4.13 设R为A上的关系，n为自然数：

1. R⁰ = {<x,x> | x ∈ A} = I_A
2. Rⁿ⁺¹ = Rⁿ ∘ R

注意：

• 对于A上的任何关系R₁和R₂都有 R₁⁰ = R₂⁰ = I_A
• 对于A上的任何关系R都有 R¹ = R

幂运算的方法

• 集合表示：计算Rⁿ就是n个R合成
• 矩阵表示：就是矩阵相乘，采用逻辑加：
  • 1+1=1, 1+0=0+1=1, 0+0=0

例3：设A = {a, b, c, d}, R = {<a,b>, <b,a>, <b,c>, <c,d>}，求R的各次幂, 分别用矩阵和关系图表示。

解：
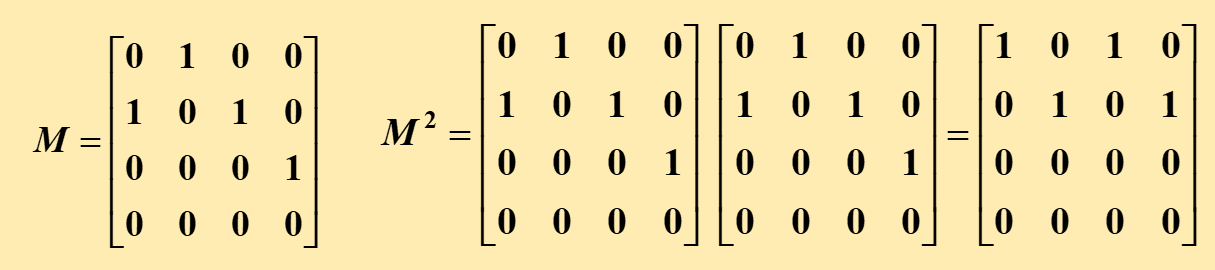
R的关系矩阵为：

同理R³和R⁴的矩阵是：

通过矩阵乘法计算：

• R²的关系矩阵M² = M × M
• R³的关系矩阵M³ = M² × M
• R⁴的关系矩阵M⁴ = M³ × M

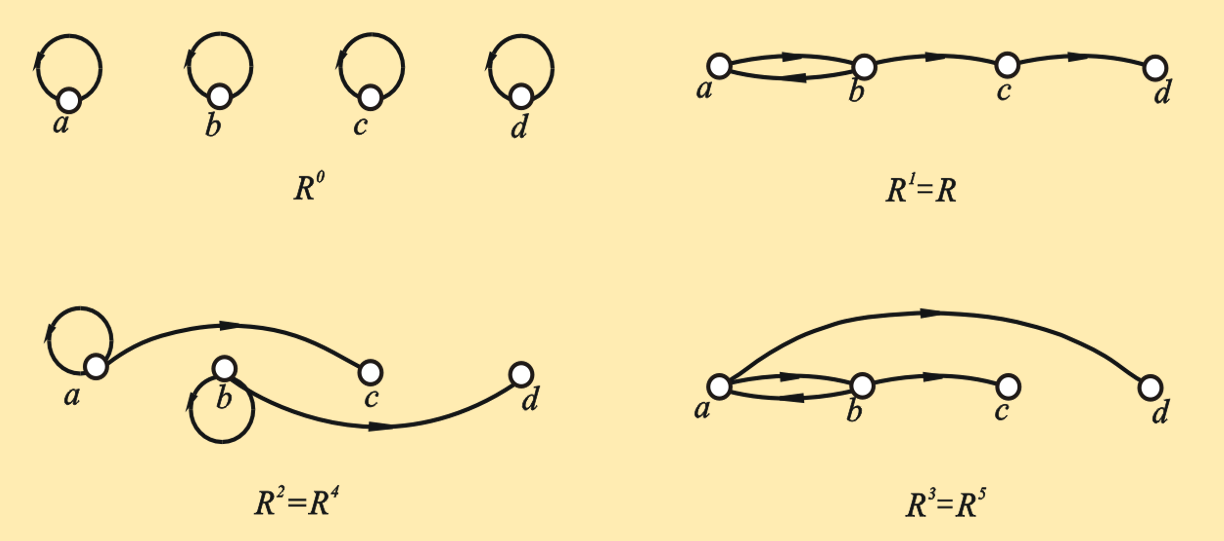
计算发现M⁴ = M²，即R⁴ = R²，因此：

• R² = R⁴ = R⁶ = ⋯
• R³ = R⁵ = R⁷ = ⋯

R⁰ = I_A的关系矩阵是单位矩阵

用关系图的方法得到R⁰, R¹, R², R³,…的关系图如下图所示

幂运算的性质

定理4.4 设A为n元集，R是A上的关系，则存在自然数s和t，使得Rˢ = Rᵗ。

证明：R为A上的关系，由于|A|=n，A上的不同关系只有2ⁿ^²个。当列出R的各次幂R⁰, R¹, R², …, 2ⁿ^², …时，必存在自然数s和t使得Rˢ = Rᵗ。

定理4.5 设R是A上的关系，m, n ∈ ℕ：

1. Rᵐ ∘ Rⁿ = Rᵐ⁺ⁿ
2. (Rᵐ)ⁿ = Rᵐⁿ

证明：
(1) 对任意给定的m ∈ ℕ，施归纳于n：

• 若n=0：Rᵐ ∘ R⁰ = Rᵐ ∘ I_A = Rᵐ = Rᵐ⁺⁰

• 假设Rᵐ ∘ Rⁿ = Rᵐ⁺ⁿ，则：

  \[Rᵐ∘Rᵐ⁺⁰ = Rᵐ∘(Rⁿ∘R) = (Rᵐ∘Rⁿ)∘R = Rᵐ⁺ⁿ∘R = Rᵐ⁺ⁿ⁺¹\]

∴ 对一切$m, n ∈ ℕ$有$Rᵐ ∘ Rⁿ = Rᵐ⁺ⁿ$

(2) 对任意给定的m ∈ ℕ，施归纳于n：

• 若n=0：(Rᵐ)⁰ = I_A = R⁰ = Rᵐ˙⁰

• 假设(Rᵐ)ⁿ = Rᵐⁿ，则：

  \[(Rᵐ)ⁿ⁺¹ = (Rᵐ)ⁿ∘Rᵐ = (Rᵐⁿ)∘Rᵐ = Rᵐⁿ⁺ᵐ = Rᵐ(ⁿ⁺¹)\]

∴ 对一切$m, n ∈ ℕ$有$(Rᵐ)ⁿ = Rᵐⁿ$

定理4.6 设R是A上的关系，若存在自然数s, t (s < t)使得Rˢ = Rᵗ，则：

1. 对任何k ∈ ℕ有 Rˢ⁺ᵏ = Rᵗ⁺ᵏ
2. 对任何k, i ∈ ℕ有 Rˢ⁺ᵏᵖ⁺ⁱ = Rˢ⁺ⁱ，其中p = t-s
3. 令S = {R⁰, R¹, …, Rᵗ⁻¹}，则对于任意的q ∈ ℕ有R^q ∈ S

证明：
(1) Rˢ⁺ᵏ = Rˢ ∘ Rᵏ = Rᵗ ∘ Rᵏ = Rᵗ⁺ᵏ
(2) 对k归纳：

• 若k=0：Rˢ⁺⁰ᵖ⁺ⁱ = Rˢ⁺ⁱ

• 假设Rˢ⁺ᵏᵖ⁺ⁱ = Rˢ⁺ⁱ，其中p = t-s，则：

  \[Rˢ⁺⁽ᵏ⁺¹⁾ᵖ⁺ⁱ = Rˢ⁺ᵏᵖ⁺ⁱ⁺ᵖ = Rˢ⁺ᵏᵖ⁺ⁱ ∘ Rᵖ = Rˢ⁺ⁱ ∘ Rᵖ = Rˢ⁺ᵖ⁺ⁱ = Rˢ⁺ᵗ⁻ˢ⁺ⁱ = Rᵗ⁺ⁱ = Rˢ⁺ⁱ\]

由归纳法命题得证。

(3) 任取q ∈ ℕ：

• 若q < t，显然有R^q ∈ S
• 若q ≥ t，则存在自然数k和i使得$q = s + kp + i$，其中$0 ≤ i ≤ p-1$
  于是R^q = Rˢ⁺ᵏᵖ⁺ⁱ = Rˢ⁺ⁱ
  而$s+i ≤ s+p-1 = s+t-s-1 = t-1$
  ∴ R^q ∈ S