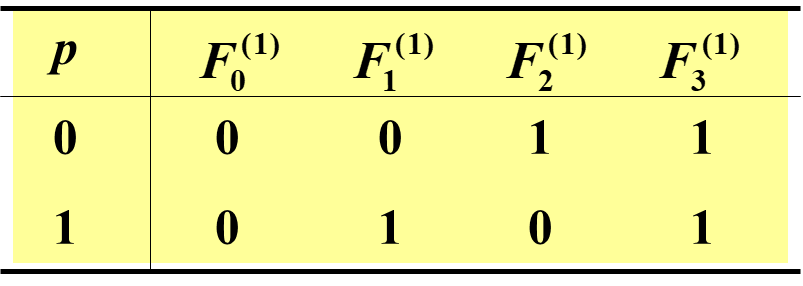离散数学-Week1
离散数学-第1周小结
数理逻辑(引言)
逻辑学也称为形式逻辑,是关于思维形态的结构及其规律的科学。
-
人们思维形态结构的过程: 概念→判断→推理
-
推理:由若干个已知的判断(前提),推出新的判断(结论)的思维过程,即从已知的信息中得出新的结论。
-
演绎推理:由一般规律推出个别事实的推理。
-
“数学方法”:建立一套有严格定义的符号体系,即建立一套形式语言,来研究形式逻辑(将文字转换为通俗的符号,用数学语言将文字符号化,所以数理逻辑也称为“符号逻辑”)。
-
数理逻辑是用数学的方法研究形式逻辑。
命题逻辑基本概念
命题与联结词
概念→判断→推理
命题的真值:
- 命题的真值只有两个:“真”或“假”。
- 命题的真值为真:一个命题所表达的判断与客观情况一致,记作T (True)。
- 命题的真值为假:一个命题所表达的判断与客观情况不一致,记作F (False)。
判断一句话是否是命题有两个关键:
- 是陈述句;
- 有且只有一个真值。
注意: 感叹句、祈使句、疑问句都不是命题
陈述句中的悖论以及判断结果不惟一确定的也不是命题
- 命题: 判断结果惟一的陈述句
- 命题的真值: 判断的结果,真或假
- 真命题: 真值为真的命题
- 假命题: 真值为假的命题
简单命题(原子命题):简单陈述句构成的命题 简单命题的符号化:用p, q, r, …, pᵢ, qᵢ, rᵢ (i ≥ 1)表示 用“1”表示真,用“0”表示假
复合命题:由简单命题通过联结词联结而成的陈述句
定义2.1 “非p”(或 “p的否定”)称为p的否定式, 记作¬p, ¬称作否定联结词, 规定¬p为真当且仅当¬p为假
定义2.2 “p并且q”(或“p与q”)称为p与q的合取式, 记作p∧q, ∧称作合取联结词, 规定 p∧q为真当且仅当 p与q同时为真
定义2.3 “p或q”称作p与q的析取式,记作p∨q, ∨称作析取联结词, 并规定p∨q为假当且仅当p与q同时为假.
相容或与排斥或
例如:这件事由张三和李四中的一人去做
设 p:张三做这件事, q:李四做这件事
应符号化为 (p∧¬q) ∨ (¬p∧q)
定义2.4 “如果p,则q” 称作p与q的蕴涵式, 记作p→q, 并称p是蕴涵式的前件, q为蕴涵式的后件. →称作蕴涵联结词, 规定, p→q为假当且仅当¬p为真且q为假.
p→q 的逻辑关系: q为p的必要条件, p为q的充分条件 “如果p,则q” 的多种表述方式:
- 若p,就q
- 只要p,就q
- p仅当q
- 只有q才p
- 除非q,才p
- 除非q,否则非p
note:当p为假时,p→q为真(不管q为真, 还是为假)
定义2.5 “p当且仅当q”称作p与q的等价式, 记作p↔q, ↔称作等价联结词. 并规定p↔q为真当且仅当p与q同时为真或同时为假。 p↔q的逻辑关系: p与q互为充分必要条件。
基本复合命题的真值
| p | q | ¬p | p∧q | p∨q | p→q | p↔q |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
联结词优先级:( ),¬, ∧, ∨, →, ↔
同级按从左到右的顺序进行
命题公式及其分类
合式公式
- 命题常项: 简单命题
- 命题变项: 取值0(真)或1(假)的变元
定义2.6 合式公式 (命题公式, 公式) 递归定义如下:
- 单个命题常项或变项是合式公式,并称作原子合式公式
- 若A是合式公式, 则(¬A)也是合式公式
- 若A, B是合式公式, 则(A∧B), (A∨B), (A→B), (A↔B)也是合式公式
- 只有有限次地应用1~3形成的符号串才是合式公式
说明:
1. 元语言符号与对象语言符号
2. 在不影响运算顺序时, 括号可以省去
合式公式的层次 定义2.7
- 单个命题变项或命题常项是0层公式
- 称A是n+1(n≥0)层公式是指下面情况之一:
- A=¬B, B是n层公式
- A=B∧C, 其中B,C分别为i层和j层公式, 且 n=max(i, j)
- A=B∨C, 其中B,C的层次及n同(b)
- A=B→C, 其中B,C的层次及n同(b)
- A=B↔C, 其中B,C的层次及n同(b)
例如
p:0层
¬p:1层
¬p→q:2层
¬(p→q)↔r:3层
((p→q)→r)↔(¬r∨s):4层
公式的赋值 定义2.8 设p1, p2, … , pn是出现在公式A中全部的命题变项, 给 p1, p2, … , pn指定一组真值, 称为对A的一个赋值或解释。使公式为真的赋值称作成真赋值, 使公式为假的赋值称作成假赋值。
说明:
(1) 赋值记作 a = a₁a₂…aₙ,aᵢ = 0 或 1,诸 aᵢ 之间不加标点符号
(2) 通常赋值与命题变项之间按下标或字母顺序对应,即:
- 当 A 的全部命题变项为 p₁, p₂, …, pₙ 时,给 A 赋值 a₁a₂…aₙ 是指 p₁ = a₁, p₂ = a₂, …, pₙ = aₙ
- 当 A 的全部命题变项为 p, q, r, … 时,给 A 赋值 a₁a₂a₃… 是指 p = a₁, q = a₂, r = a₃, …
真值表: 命题公式在所有可能的赋值下的取值的列表 含n个变项的公式有2n个赋值
命题公式的分类 重言式(永真式): 无成假赋值的命题公式 矛盾式(永假式): 无成真赋值的命题公式 可满足式: 非矛盾式的命题公式
注意: 重言式是可满足式,但反之不真。
命题逻辑等值演算
等值式
定义2.11 若等价式A↔B是重言式, 则称A与B等值, 记作A⇔B, 并称A⇔B是等值式
说明:
(1) ⇔是元语言符号, 不要混同于↔和=
(2) A与B等值当且仅当A与B在所有可能赋值下的真值都相同, 即A与B有相同的真值表
(3) n个命题变项的真值表共有22n个, 故每个命题公式都有无穷多个等值的命题公式
(4) 可能有哑元出现. 在B中出现, 但不在A中出现的命题变项称作A的哑元. 同样,在A中出现, 但不在B中出现的命题变项称作B的哑元. 哑元的值不影响命题公式的真值
判断A与B是否等值:
- 真值表法
- 基本等值式
- 双重否定律 (Double Negation Law)
公式: ¬¬A ⇔ A
解释: 两个否定等价于肯定。例如,“不是不喜欢”等价于“喜欢”。
示例: 如果 A 表示“下雨”,那么 ¬¬A 表示“不是不下雨”,即“下雨”。
- 双重否定律 (Double Negation Law)
-
幂等律 (Idempotent Law)
公式: A ∨ A ⇔ A, A ∧ A ⇔ A
解释: 一个命题与自身进行“或”或“且”操作,结果等于自身。重复的命题不会改变真值。
示例:
A ∨ A: “今天下雨或今天下雨”等价于“今天下雨”。
A ∧ A: “今天下雨且今天下雨”等价于“今天下雨”。 -
交换律 (Commutative Law)
公式: A ∨ B ⇔ B ∨ A, A ∧ B ⇔ B ∧ A
解释: “或”和“且”操作满足交换律,即操作数的顺序不影响结果。
示例:
A ∨ B: “下雨或刮风”等价于“刮风或下雨”。
A ∧ B: “下雨且刮风”等价于“刮风且下雨”。 -
结合律 (Associative Law)
公式: (A ∨ B) ∨ C ⇔ A ∨ (B ∨ C), (A ∧ B) ∧ C ⇔ A ∧ (B ∧ C)
解释: “或”和“且”操作满足结合律,即分组方式不影响结果。注意,这对于“异或”等操作不一定成立。
示例:
(A ∨ B) ∨ C: “(下雨或刮风)或多云”等价于“下雨或(刮风或多云)”。
(A ∧ B) ∧ C: “(下雨且刮风)且多云”等价于“下雨且(刮风且多云)”。 -
分配律 (Distributive Law)
公式:
A ∨ (B ∧ C) ⇔ (A ∨ B) ∧ (A ∨ C)
A ∧ (B ∨ C) ⇔ (A ∧ B) ∨ (A ∧ C)
解释: 类似于算术中的分配律,“或” over “且”以及“且” over “或”。
示例: A ∨ (B ∧ C): “下雨或(刮风且多云)”等价于“(下雨或刮风)且(下雨或多云)”。
A ∧ (B ∨ C): “下雨且(刮风或多云)”等价于“(下雨且刮风)或(下雨且多云)”。 -
德摩根律 (De Morgan’s Law)
公式:
¬(A ∨ B) ⇔ ¬A ∧ ¬B
¬(A ∧ B) ⇔ ¬A ∨ ¬B
解释: “或”的否定等价于否定的“且”,“且”的否定等价于否定的“或”。这是逻辑否定中的重要定律。
示例:
¬(A ∨ B): “并非(下雨或刮风)”等价于“不下雨且不刮风”。
¬(A ∧ B): “并非(下雨且刮风)”等价于“不下雨或不刮风”。 -
吸收律 (Absorption Law)
公式:
A ∨ (A ∧ B) ⇔ A
A ∧ (A ∨ B) ⇔ A
解释: 一个命题与另一个命题的合取或析取相结合时,可以被“吸收”回自身。这常用于简化表达式。
示例:
A ∨ (A ∧ B): “下雨或(下雨且刮风)”等价于“下雨”。
A ∧ (A ∨ B): “下雨且(下雨或刮风)”等价于“下雨”。 -
零律 (Domination Law)
公式: A∨1⇔1A∨1⇔1, A∧0⇔0A∧0⇔0
解释: 无论命题A的真值如何,A与真的析取(或)总是真;A与假的合取(且)总是假。
示例:
A∨1A∨1: 如果A为真,则真或真为真;如果A为假,则假或真为真。所以结果总是真。
A∧0A∧0: 如果A为真,则真且假为假;如果A为假,则假且假为假。所以结果总是假。 -
同一律 (Identity Law)
公式: A∨0⇔AA∨0⇔A, A∧1⇔AA∧1⇔A
解释: A与假的析取(或)等于A本身;A与真的合取(且)也等于A本身。
示例:
A∨0A∨0: 如果A为真,则真或假为真;如果A为假,则假或假为假。所以结果总是A。
A∧1A∧1: 如果A为真,则真且真为真;如果A为假,则假且真为假。所以结果总是A。 -
排中律 (Law of Excluded Middle)
公式: A∨¬A⇔1A∨¬A⇔1
解释: A或非A总是真。这意味着一个命题要么为真,要么为假,没有第三种可能。
示例:
A∨¬AA∨¬A: 如果A为真,则真或假为真;如果A为假,则假或真为真。所以总是真。 -
矛盾律 (Law of Contradiction)
公式: A∧¬A⇔0A∧¬A⇔0
解释: A且非A总是假。这意味着一个命题不能同时为真和假。
示例:
A∧¬AA∧¬A: 如果A为真,则真且假为假;如果A为假,则假且真为假。所以总是假。 -
蕴涵等值式 (Implication Equivalence)
公式: A→B⇔¬A∨BA→B⇔¬A∨B
解释: 蕴含A→B等价于非A或B。这是蕴含的常见定义,表示如果A为真则B必须真,但如果A为假,则无论B如何,蕴含都为真。
示例:
A→BA→B: 例如,“如果下雨,地湿”等价于“不下雨或地湿”。 -
等价等值式 (Equivalence Equivalence)
公式: A↔B⇔(A→B)∧(B→A)A↔B⇔(A→B)∧(B→A)
解释: 双条件A↔B等价于(A→B)且(B→A)。这意味着A和B互相蕴含,即A和B同时为真或同时为假。
示例:
A↔BA↔B: 例如,“一个数是偶数当且仅当它能被2整除”等价于“如果它是偶数,那么它能被2整除,并且如果它能被2整除,那么它是偶数”。 -
假言易位 (Contraposition)
公式: A→B⇔¬B→¬AA→B⇔¬B→¬A
解释: 蕴含A→B等价于其逆否命题:如果非B则非A。这是一种常见的推理形式。
示例:
A→BA→B: 例如,“如果下雨,地湿”等价于“如果地不湿,则没下雨”。 -
等价否定等值式 (Equivalence Negation Equivalence)
公式: A↔B⇔¬A↔¬BA↔B⇔¬A↔¬B
解释: A等价于B当且仅当非A等价于非B。这意味着A和B的真值相同,从而非A和非B的真值也相同。
示例:
A↔BA↔B: 例如,“A是真当且仅当B是真”等价于“A是假当且仅当B是假”。 -
归谬论 (Reductio ad Absurdum)
公式: (A→B)∧(A→¬B)⇔¬A(A→B)∧(A→¬B)⇔¬A
解释: 如果A既蕴含B又蕴含非B,则A必须为假。这是一种反证法,通过导出矛盾来否定A。
示例:
(A→B)∧(A→¬B)(A→B)∧(A→¬B): 例如,假设“如果A成立,则B成立”和“如果A成立,则B不成立”同时为真,那么A必然为假。因为如果A为真,会导致B和非B同时为真,这是不可能的。
等值演算
等值演算: 由已知的等值式推演出新的等值式的过程
置换规则: 若A⇔B, 则Φ(B)⇔Φ(A)
等值演算不能直接证明两个公式不等值。证明两个公式不等值的基本思想是找到一个赋值使一个成真, 另一个成假。
真值函数
定义2.12 称F:{0,1}ⁿ→{0,1}为n元真值函数
n元真值函数共有22n个
每一个命题公式对应于一个真值函数
每一个真值函数对应无穷多个命题公式
真值函数
- 定义:一个n(n≥1)阶笛卡尔积{0,1}n 到{0,1}的函数称为一个n元真值函数,记作:{0,1}ⁿ→{0,1}。
- 笛卡尔积:笛卡尔积的符号化为:A×B={(x,y)|x∈A∧y∈B}。假设集合A={a, b},集合B={0, 1, 2},则两个集合的笛卡尔积为{(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}。
n个命题变项,共有2ⁿ个可能的赋值。对于每个赋值,真值函数的函数值非0即1。于是n个命题变元共可以形成22n个不同的真值函数。每个真值函数对应一个真值表(只看最后一列,不计中间的计算过程),也对应无穷多个命题公式,这些公式彼此都是等值的,它们中的每个都是这个真值函数的一个表达形式。
联结词完备集
定义2.13 设S是一个联结词集合, 如果任何n(n≥1)元真值函数都可以由仅含S中的联结词构成的公式表示,则称S是联结词完备集。
指具有下列性质的联结词的集合:对于任给的一个真值表,存在一个仅由该集中联结词构成的命题演算公式,使得该公式所对应的真值表恰为该真值表。
定理2.1:以下都是完备集:
- S₁ = {¬, ∧, ∨, →, ↔}
- S₂ = {¬, ∧, ∨, →} A↔B ⇔ (A→B)∧(B→A)
- S₃ = {¬, ∧, ∨} A→B ⇔ ¬A∨B
- S₄ = {¬, ∧} A∨B ⇔ ¬¬(A∨B)(双重否定律)⇔ ¬(¬A∧¬B) (德摩根律:¬(A∨B) ⇔ ¬A∧¬B,对其取否定)
- S₅ = {¬, ∨} A∧B ⇔ ¬¬(A∧B)(双重否定律)⇔ ¬(¬A∨¬B) (德摩根律:¬(A∧B) ⇔ ¬A∨¬B,对其取否定)
- S₆ = {¬, →} A∨B ⇔ ¬¬A∨B(对第一个A使用双重否定律)⇔ ¬A→B(蕴涵等值式:¬A→B ⇔ ¬¬A∨B ⇔ A∨B)
复合联结词
-
与非式:p↑q ⇔ ¬(p∧q)(↑称为与非联结词)
p↑q为真当且仅当p,q不同时为真 -
或非式:p↓q ⇔ ¬(p∨q)(↓称为或非联结词)
p↓q为真当且仅当p,q同时为假
定理2.2: {↑}和{↓}都是联结词完备集
1. 证明{↑}是联结词完备集
-
用↑表示否定联结词¬
¬p
⇔ ¬(p∧p) (因为p∧p ⇔ p,幂等律)
⇔ p↑p (根据↑的定义:p↑q ⇔ ¬(p∧q),令q=p) -
用↑表示合取联结词∧
p∧q
⇔ ¬¬(p∧q) (双重否定律)
⇔ ¬(p↑q) (根据↑的定义:p↑q ⇔ ¬(p∧q))
⇔ (p↑q)↑(p↑q) (用↑表示¬:¬x ⇔ x↑x,令x=p↑q)
2. 证明{↓}是联结词完备集
-
用↓表示否定联结词¬
¬p
⇔ ¬(p∨p) (因为p∨p ⇔ p,幂等律)
⇔ p↓p (根据↓的定义:p↓q ⇔ ¬(p∨q),令q=p) -
用↓表示析取联结词∨
p∨q
⇔ ¬¬(p∨q) (双重否定律)
⇔ ¬(p↓q) (根据↓的定义:p↓q ⇔ ¬(p∨q))
⇔ (p↓q)↓(p↓q) (用↓表示¬:¬x ⇔ x↓x,令x=p↓q)